The scientific Python ecosystem
Contents
8. The scientific Python ecosystem¶
Python has an excellent eco-system of scientific computing tools. What do we
mean when we say “scientific computing”? There’s no one definition, but we
roughly mean those parts of computing that allow us to work with scientific
data. Data that represents images or time-series from neuroimaging experiments
definitely under that definition. It’s also often called “numerical computing”,
because these data are often stored as numbers. A common structure for numerical
computing is that of an array. An array is an ordered collection of items that
are stored such that a user can access one or more items in the array. The
numpy Python library provides an implementation of an
array data structure that is both powerful and light-weight.
What do we mean by “eco-system”? This means that many different individuals and organizations develop software that interoperates to perform the various scientific computing tasks that they need to perform. Tools compete for users and developers’ attention and mind-share, but more often they might coordinate. No one entity manages this coordination. In that sense, the collection of software tools that exists in Python is more like an organically evolving ecosystem than a centrally-managed organization. One place in which the ecosystem comes together as a community is an annual conference called “Scientific Computing in Python”, which takes place in Austin, Texas every summer.
8.1. Numerical computing in Python¶
8.1.1. From naive loops to n-dimensional arrays¶
In many disciplines, data analysis consists largely of the analysis of tabular data. This means two-dimensional tables where data are structured into rows and columns, with each observation typically taking up a row, and each column representing a single variable. Neuroimaging data analysis also often involves tabular data, and we’ll spend a lot of time in Section 9 discussing the tools Python provides for working efficiently with tabular data.
However, one of the notable features of neuroscience experiments is that datasets are often large, and naturally tend to have many dimensions. This means that data from neuroscience experiments is often stored in big tables of data called arrays. Much like Python lists or tuples, the items in an array follow a particular order. But in contrast to a list or a tuple, they can have multiple dimensions: arrays can have one dimension (for example a time-series from a single channel of an EEG recording), two dimensions (for example all the time-series from multiple EEG channels recorded simultaneously or a single slice from an MRI image), three dimensions (for example, an anatomical scan of a human brain), four dimensions (for example, an fMRI dataset with the three spatial dimensions and time-points arranged as a series of volumes along the last dimension) or even more.
In all of these cases, the arrays are continuous. That means that there are no holes in an array, where nothing is stored. They are also homogeneous, which means that all of the items in an array are of the same numerical data type. That is, if one number stored in the array is a floating point number, all numbers in the array will be represented in their floating point representation. It also means that the dimensions of the array are predictable. If the first channel of the EEG time-series has 20,000 time-points in it, the second channel would also have 20,000 time-points in it. If the first slice of an MRI image has 64-by-64 voxels, other slices in the MRI image would also have 64-by-64 voxels.
To understand why this is challenging, let’s consider a typical fMRI study, in which participants lie in the scanner, while their brain responses are measured. Suppose we have 20 participants, each scanned for roughly 30 minutes, with a repetition time (TR) -— i.e., the duration of acquisition of each fMRI volume -— of 1 second. If the data are acquired at an isotropic spatial resolution of 2mm (i.e., each brain “voxel”, or 3-dimensional pixel is 2 mm along each dimension), then the resulting dataset might have approximately 20 x 1800 x 100 x 100 x 100 = 36 billion observations. That’s a lot of data! Moreover, each subject’s data has a clear 4 dimensional structure — the 3 spatial dimensions, plus time. If we wanted to, we could also potentially represent subjects as the 5th dimension, though that involves some complications, since at least initially, different subjects’ brains won’t be aligned with one another —- we’d need to spatially register them for that (we’ll learn more about that in Section 16).
This means that a single subject’s data would look a little bit like the 4-dimensional example that we looked at just a moment ago.
We will typically want to access this data in pretty specific ways. That is, rather than applying an operation to every single voxel in the brain, at every single point in time, we usually want to pull out specific slices of the data, and only apply an operation to those slices. Say for example we’re interested in a voxel in the amygdala. How would we access only that voxel, at every time point?
A very naive approach that we could implement in pure Python would be to store all our data as a nested series of Python lists: each element in the first list would be a list containing data for one time point; each element within the list for each time point would itself be a list containing the 2d slices at each x-coordinate; and so on. Then we could write a series of 4 nested for-loops to sequentially access every data point (or voxel) in our array. For each voxel we inspect, we could then determine whether the voxel is one we want to work with, and if so, apply some operation to it.
Basically, we’d have something like this (note that this is just pseudocode, not valid Python code, and you wouldn’t be able to execute this snippet!):
for t in time:
for x in t:
for y in x:
for z in y:
if z is in amygdala:
apply_my_function(z)
Something like the above would probably work just fine. But it would be very inefficient, and might take a while to execute. Even if we only want to access a single amygdala voxel at each timepoint (i.e., 1800 data points in total, if we stick with our resting state example from above), our naive looping approach still requires us to inspect every single one of the 1.8 billion voxels in our dataset —- even if all we’re doing for the vast majority of voxels is deciding that we don’t actually need to use that voxel in our analysis! This is, to put it mildly, A Bad Thing.
Computer scientists have developed a notation for more precisely describing how much of a bad thing it is: Big O notation, which gives us a formal way of representing the time complexity of an algorithm. In Big O notation, the code above runs in \(O(n^4)\) time. Meaning, for any given dimension size \(n\) (we assume for simplicity that \(n\) is the same for all dimensions), we need to perform on the order of \(n^4\) computations. To put this in perspective, just going from \(n = 2\) to \(n = 4\) means that we go from \(2^4 = 16\) to \(4^4 = 256\) operations. You can see how this might start to become problematic as \(n\) gets large.
The lesson we should take away from this is that writing naive Python loops just to access the values at a specific index in our dataset is a bad idea.
8.1.2. Towards a specialized array structure¶
What about list indexing? Fortunately, since we’ve already covered list indexing in Python, we have a better way to access the amygdala data we want. We know that the outer dimension in our nested list represents time, and we also know that the spatial index of the amygdala voxel we want will be constant across time points. This means that instead of writing a 4-level nested for-loop, we can do the job in just a single loop. If we know that the index of the amygdala voxel we want in our 3-d image is [20, 18, 32], then the following code suffices (again note that this code can’t be executed):
amygdala_values = []
for t in dataset:
amygdala_values.append(t[20][18][32])
That’s a big improvement, in terms of time complexity. We’ve gone from an \(O(n^4)\) to an \(O(n)\) algorithm. The time our new algorithm takes to run is now linear in the number of timepoints in our dataset, rather than growing as a polynomial function of it.
Unfortunately, our new approach still isn’t great. One problem is that performance still won’t be so good, because Python isn’t naturally optimized for the kind of operation we just saw -— indexing repeatedly into nested lists. For one thing, Python is a dynamically typed language, so there will be some overhead involved in accessing each individual element (because the interpreter has to examine the object and determine its type), and this can quickly add up if we have millions or billions of elements.
The other big limitation is that, even if lists themselves were super fast to
work with, the Python standard library provides limited functionality for doing
numerical analysis on them. There are a lot of basic numerical operations we
might want to apply to our data that would be really annoying to write using
only the built-in functionality of Python. For example, Python lists don’t
natively support matrix operations, so if we wanted to multiply one matrix
(represented as a list of lists) by another, we’d probably need to write out a
series of summations and multiplications ourselves inside for-loops. And that
would be completely impractical given how basic and common an operation matrix
multiplication is (not to important for our point now, but if you’re wondering
what a matrix multiplication is, you can see a formal definition in
matmul).
The bottom line is that, as soon as we start working with large, or highly structured datasets —- as is true of most datasets in neuroimaging —- we’re going to have to look beyond what Python provides us in its standard library. Lists just aren’t going to cut it; we need some other kind of data structure —- one that’s optimized for numerical analysis on large, N-dimensional datasets. This is where numpy comes into play.
8.2. Introducing Numpy¶
Numpy is the backbone of the numerical and scientific computing stack in Python; many of the libraries we’ll cover in this book (pandas, scikit-learn, etc.) depend on it internally. Numpy provides many data structures optimized for efficient representation and manipulation of different kinds of high-dimensional data, as well as an enormous range of numerical tools that help us work with those structures.
8.2.1. Importing numpy¶
Recall that the default Python namespace contains only a small number of
built-in functions. To use any other functionality, we need to explicitly import
it into our namespace. Let’s do that for Numpy. The library can be imported
using the import key word. We use import numpy as np to create a short name
for the library that we can refer to. Everything that is in numpy will now be
accessible through the short name np. Importing the library specifically as
np is not a requirement, but it is a very strongly-held convention and when
you read code that others have written, you will find that this the form that is
very often used.
import numpy as np
8.2.2. Data is represented in arrays¶
The core data structure in Numpy is the n-dimensional array (or ndarray). As
the name suggests, an ndarray is an array with an arbitrary number of
dimensions. Unlike Python lists, Numpy arrays are homogeneously typed -—
meaning, every element in the array has to have the same data type. You can have
an array of floats, or an array of integers, but you can’t have an array that
mixes floats and integers. This is exactly what we described above: a
homogeneous dense table that holds items in it.
8.2.3. Creating ndarrays¶
Like any other Python object, we need to initialize an ndarray before we can
do anything with it. Numpy provides us with several ways to create new arrays.
Let’s explore a couple.
8.2.3.1. Initializing an array from an existing list¶
Let’s start by constructing an array from existing data. Assume we have some
values already stored in a native Python iterable object (typically, a list;
“iterable” means that it is an object that we can iterate over with a for loop,
see Section 5.5.2). If we want to convert that object to an ndarray so that
we can perform more efficient numerical operations on it, we can pass the object
directly to the np.narray() function. In a relatively simple case, the input
to the np.array function is a sequence of items, a list that holds some
integers.
list_of_numbers = [1, 1, 2, 3, 5]
arr1 = np.array(list_of_numbers)
print(arr1)
[1 1 2 3 5]
The result still looks a lot like a list of numbers, but let’s look at some of the attributes that this variable has that are not available in lists.
print("The shape of the array is", arr1.shape)
print("The dtype of the array is", arr1.dtype)
print("The size of each item is", arr1.itemsize)
print("The strides of the array is", arr1.strides)
The shape of the array is (5,)
The dtype of the array is int64
The size of each item is 8
The strides of the array is (8,)
The shape of an array is its dimensionality. In this case, the array is
one-dimensional (like the single channel of EEG data in the example above). All
of the items in this array are integers, so we can use an integer representation
as the dtype of the array. This means that each element of the array takes up 8
bytes of memory. Using 64-bit integers, we can represent the numbers from
-9223372036854775808 to 9223372036854775807. And each one would take up 8 bytes
of memory in our computer (which are 64 bits). This also explains the strides.
Strides are the number of bytes in memory that we would have to skip to get to
the next value in the array. Because the array is packed densely in a contiguous
segment of memory, to get from the value 1 to the value 2, for example, we
have to skip 8 bytes.
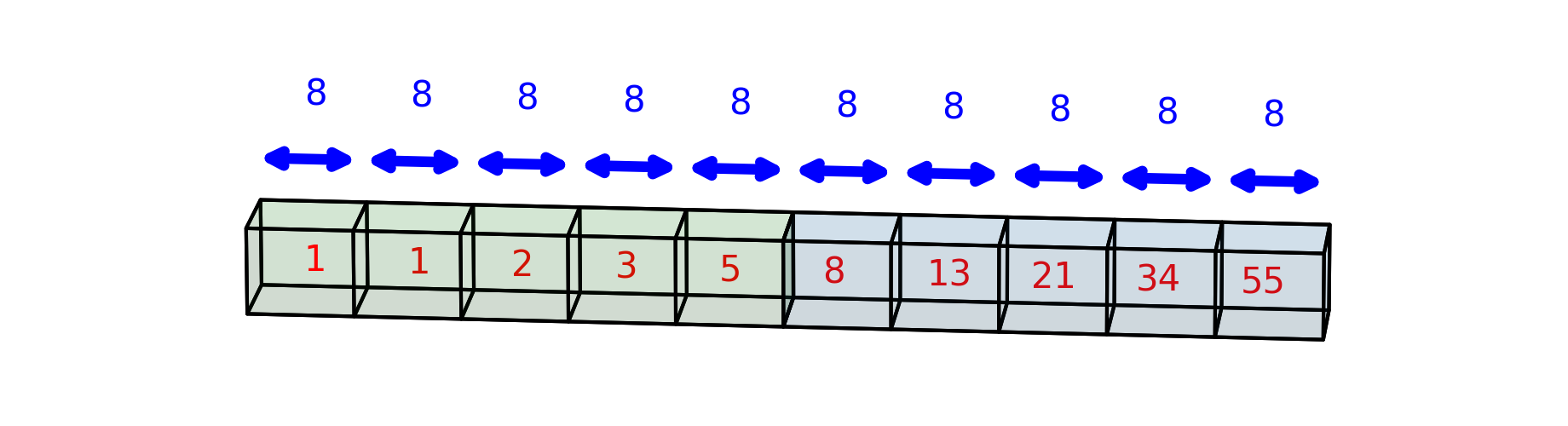
Remember that the data we would like to represent in arrays can have multiple dimensions. Numpy is pretty good about figuring out what kind of array we want based on the input data; for example, if we pass in a list of lists, where each of the inner lists has the same number of elements, Numpy will infer that we want to construct a 2-dimensional array
list_of_lists = [[1, 1, 2, 3, 5], [8, 13, 21, 34, 55]]
arr2 = np.array(list_of_lists)
print(arr2)
print("The shape of this array is", arr2.shape)
print("The dtype of this array is", arr2.dtype)
print("The size of each item is", arr2.itemsize)
print("The strides of this array are", arr2.strides)
[[ 1 1 2 3 5]
[ 8 13 21 34 55]]
The shape of this array is (2, 5)
The dtype of this array is int64
The size of each item is 8
The strides of this array are (40, 8)
Now, the shape of the array is 2 items: the first is the number of lists in the
array (2) and the second is the number of items in each list (5). You can also
think of that as rows (2 rows) and columns (5 columns), because each item in the
first row of the array has an item matching it in terms of its column in the
second row. For example, the number 2 in the first row is equivalent to the
number 21 in the second row in that they are both the third item in their
particular rows. Or, in other words, they share the third column in the array.
The items are still each 8 bytes in size, but now there are two items in the
strides: (40, 8). The first item tells us how many bytes we have to move to
get from one row to the next row (for example, from the 2 in the first row to
the 21 in the second row). That’s because the part of the computer’s memory in
which the entire array is stored is contiguous and linear. Here, we’ve drawn
this contiguous bit of memory, such that the part that represents the first row
of the array is green and the part that represents the second row of the array
is blue.
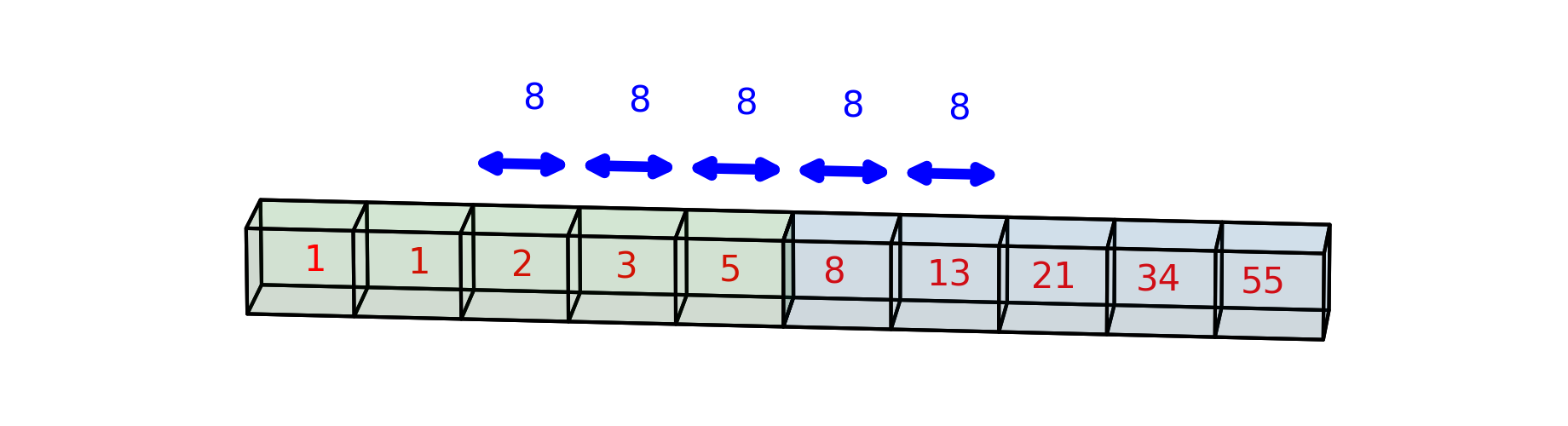
The first time you see a printed representation of a Numpy array, as in the above output, it might look a little confusing. But the visual representation closely resembles what we’d see if we were to print the nested list in Python. In the 2-dimensional case above, the elements of the outer list are the values along the first dimension, and each inner list gives the values along the second dimension. This ends up giving us a nice tabular representation, where, at least for small arrays, we can just read off the values from the output. For example, the first row of the array contains the values [1, 1, 2, 3, 5]; the second column of the array contains the values [1, 13]; and so on.
8.2.3.2. Exercise¶
Extend the above principle into 3 dimensions: create a list of list of lists, initialize an array from the list, and print into the screen. Make sure you understand how the values displayed visually map onto the dimensions of the array.
8.2.3.3. Initializing an empty array¶
Alternatively, we can construct a new array from scratch and fill it with some
predetermined value – most commonly zero. We can do this easily in Numpy using
the conveniently - named np.zeros function. In many practical applications, we
can think of this as an “empty” array (though technically we could also create a
truly empty array that has no assigned values using the np.empty function).
The zeros function takes a mandatory shape tuple as its first argument; this
specifies the dimensions of the desired array.
arr_2d = np.zeros((5, 10))
print("The shape of this array is", arr_2d.shape)
print("The dtype of this array is", arr_2d.dtype)
print("The size of each item is", arr_2d.itemsize)
print("The strides of this array are", arr_2d.strides)
arr_3d = np.zeros((2, 4, 8))
print("The shape of this array is", arr_3d.shape)
print("The dtype of this array is", arr_3d.dtype)
print("The size of each item is", arr_3d.itemsize)
print("The strides of this array are", arr_3d.strides)
The shape of this array is (5, 10)
The dtype of this array is float64
The size of each item is 8
The strides of this array are (80, 8)
The shape of this array is (2, 4, 8)
The dtype of this array is float64
The size of each item is 8
The strides of this array are (256, 64, 8)
8.2.3.4. Exercise¶
Can you explain the outputs of the previous code cell? What does the first item in the strides represent in each case?
8.2.4. Neuroscience data is stored in arrays¶
As we described above, many different kinds of neuroscience data are naturally
stored in arrays. To demonstrate this, let’s look at some neuroscience data that
we’ve stored in an array. We’ve stored some data from an fMRI experiment in a
Numpy array, you can load it using our the load_data utility function from the
nsdlib software library that we have implemented:
from ndslib import load_data
This load_data function takes as arguments the name of the dataset that we
would like to download and alternatively also the name of a file that we would
like to save the data into (for reuse). The npy file format is a format that
was developed specifically to store Numpy arrays and that’s all that it knows
how to store. When you load one of these files, you can assign into a variable
the contents of the array that was stored in the file.
bold = load_data("bold_numpy", fname="bold.npy")
print("The shape of the data is", bold.shape)
print("The dtype of the data is", bold.dtype)
print("The itemsize of the data is", bold.itemsize)
print("The strides of the data is", bold.strides)
The shape of the data is (64, 64, 25, 180)
The dtype of the data is float64
The itemsize of the data is 8
The strides of the data is (8, 512, 32768, 819200)
This data is a little bit more complicated than the arrays you have seen so far.
It has 4 dimensions: the first two dimensions are the inplane dimensions of each
slice: 64 by 64 voxels. The next dimension is the slice dimension: 25 slices.
Finally, the last dimension is the time-points that were measured in the
experiment. The dtype of this array is float64. These floating point numbers
are what computers use to represent real numbers. Each one of these items also
uses up 64 bits, or 8 bytes, so that’s the item size here as well. Just like the
shape, there are 4 strides: the first item in the strides tells how far we need
to go to get from one voxel to another voxel in the same row, in the same slice,
in the same time-point. The second stride (512) tells us how far we would have
to go to find the same voxel in the same slice and time-point, but one row over.
That’s 64 times 8. The next one is about finding the same voxel in a neighboring
slice. Finally the large one at the end is about finding the same slice in the
next time step. That large number is equal to 64 by 64 by 25 (the number of
voxels in each time point) by 8 (the number of bytes per element in the array).
8.2.5. Indexing is used to access elements of an array¶
We’ve seen how we can create arrays and describe them; now let’s talk about how we can get data in and out of arrays. We already know how to index Python lists, and array indexing in Python will look quite similar. But Numpy indexing adds considerably more flexibility and power, and developing array indexing facility is a critical step towards acquiring general proficiency with the package. Let’s start simple: accessing individual items in a one-dimensional array looks a lot like indexing into a list (see Section 5.3.1.2). For example, the first item in the one-dimensional array we saw earlier, you would do the following:
arr1[0]
1
or if you want the second element, you would do something like this (don’t forget that Python uses 0-based indexing!):
arr1[1]
1
Numpy arrays also support two other important syntactic conventions that are also found in Python lists: indexing from the end of the array, and “slicing” the array to extract multiple contiguous values.
To index from the end, we use the minus sign (-):
arr1[-2]
3
This gives us the 2nd-from-last value in the array. To slice an array, we use the colon (:) operator, passing in the positions we want to start and end at:
arr1[2:5]
array([2, 3, 5])
As in lists, the start index is inclusive and the end index is exclusive (i.e., in the above example, the resulting array includes the value at position 2, but excludes the one at position 6). We can also omit the start or end indexes, in which case, Numpy will return all positions up to, or starting from, the provided index. For example, to get the first 4 elements:
arr1[:4]
array([1, 1, 2, 3])
8.2.6. Indexing in multiple dimensions¶
Once we start working with arrays with more than one dimension, indexing gets a little more complicated. Both because the syntax is a little different, and because there’s a lot more we can do with multi-dimensional arrays.
For example, if you try one of these operations with a two-dimensional array, something funny will happen:
arr2[0]
array([1, 1, 2, 3, 5])
It looks like the first item of a two-dimensional array is the entire first row of that array. To access the first element in the first row, we need to use two indices, separated by a comma:
arr2[0, 0]
1
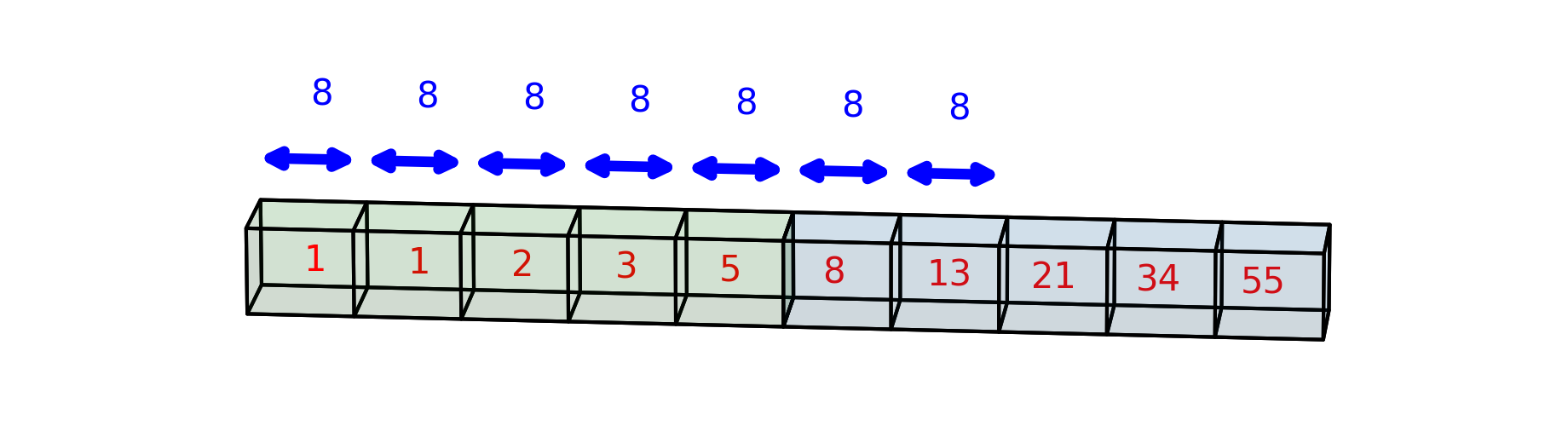
One way to think about this is that the first index points to the row and the second index points to the column, so to get the very first item in the array, we need to explicitly ask for the first column in the first row. Consider what happens when you ask for third item in the second row:
arr2[1, 2]
21
Under the hood, Python asks how many bytes into the array it would have to go to get that item. It looks at the strides and computes: 1 times the first stride = 40 plus 2 times the second stride = 40 + 16 = 56. Indeed, the third element of the second row of the array is 7 times 8 bytes into the array:
How would you access data in the BOLD array? As an example, let’s access the voxel in the very first time-point, in the very first slice, and in this slice in the first row and column:
bold[0, 0, 0, 0]
0.0
This element of the array is the very corner of the volume, so it is way outside of the part of the data that contains the brain. That is why it contains a value of 0. Instead, we can look at the voxel at the very center of the center slice:
bold[32, 32, 12, 0]
1080.0
This voxel has a value that corresponds to the intensity of the MR image in this voxel at the first time point. If we drop the last index, that would be like asking for the data in all of the time-points in that particular voxel:
bold[32, 32, 12]
array([1080., 1052., 1056., 1087., 1146., 1147., 1105., 1064., 1128.,
1089., 1095., 1049., 1109., 1051., 1074., 1073., 1112., 1086.,
1090., 1062., 1086., 1023., 1047., 1139., 1065., 1117., 1070.,
1070., 1089., 1074., 1051., 1034., 1096., 1060., 1096., 1076.,
1032., 1067., 1030., 1072., 1056., 1069., 1061., 1054., 1072.,
1072., 1035., 1018., 1116., 1056., 1051., 1084., 1075., 1080.,
1036., 1022., 1076., 1060., 1031., 1079., 1048., 1002., 1055.,
1027., 1014., 1006., 1072., 1003., 1026., 1039., 1096., 1078.,
1025., 1029., 1009., 1065., 1023., 1098., 1045., 1094., 1016.,
1015., 1027., 1020., 1030., 1049., 1034., 1053., 1018., 1038.,
1072., 1020., 1007., 1037., 1082., 1050., 1011., 1027., 972.,
992., 984., 1021., 1018., 1029., 1063., 1070., 1033., 1048.,
1052., 1040., 1007., 996., 1026., 1011., 1023., 958., 982.,
1008., 1059., 1006., 1012., 1042., 1000., 1066., 1026., 1032.,
1009., 1022., 989., 1020., 1078., 1034., 1036., 976., 1026.,
960., 1021., 1009., 1049., 1029., 1065., 1002., 1007., 1031.,
1015., 1044., 1012., 999., 1002., 979., 965., 1011., 1027.,
1013., 1012., 1022., 981., 1030., 1061., 1056., 1014., 957.,
968., 1015., 1100., 994., 1000., 973., 997., 980., 1026.,
1004., 1008., 988., 993., 1042., 1016., 1044., 1002., 1006.])
This is now a time-series of data, corresponding to the intensity of the BOLD response in the voxel at the very center of the central slice, across all time points in the measurement.
8.2.7. Slicing a dimension with “:”¶
As you saw before, we can use slicing to choose a sub-array from within our array. For example, you can slice out the time-series in the central voxel, as we just did:
bold[32, 32, 12, :]
array([1080., 1052., 1056., 1087., 1146., 1147., 1105., 1064., 1128.,
1089., 1095., 1049., 1109., 1051., 1074., 1073., 1112., 1086.,
1090., 1062., 1086., 1023., 1047., 1139., 1065., 1117., 1070.,
1070., 1089., 1074., 1051., 1034., 1096., 1060., 1096., 1076.,
1032., 1067., 1030., 1072., 1056., 1069., 1061., 1054., 1072.,
1072., 1035., 1018., 1116., 1056., 1051., 1084., 1075., 1080.,
1036., 1022., 1076., 1060., 1031., 1079., 1048., 1002., 1055.,
1027., 1014., 1006., 1072., 1003., 1026., 1039., 1096., 1078.,
1025., 1029., 1009., 1065., 1023., 1098., 1045., 1094., 1016.,
1015., 1027., 1020., 1030., 1049., 1034., 1053., 1018., 1038.,
1072., 1020., 1007., 1037., 1082., 1050., 1011., 1027., 972.,
992., 984., 1021., 1018., 1029., 1063., 1070., 1033., 1048.,
1052., 1040., 1007., 996., 1026., 1011., 1023., 958., 982.,
1008., 1059., 1006., 1012., 1042., 1000., 1066., 1026., 1032.,
1009., 1022., 989., 1020., 1078., 1034., 1036., 976., 1026.,
960., 1021., 1009., 1049., 1029., 1065., 1002., 1007., 1031.,
1015., 1044., 1012., 999., 1002., 979., 965., 1011., 1027.,
1013., 1012., 1022., 981., 1030., 1061., 1056., 1014., 957.,
968., 1015., 1100., 994., 1000., 973., 997., 980., 1026.,
1004., 1008., 988., 993., 1042., 1016., 1044., 1002., 1006.])
This is equivalent to dropping the last index. If we want to slice through all of the slices, taking the values of the central voxel in each slice, in the very first time-point, we would instead slice on the third (slice) dimension of the array:
bold[32, 32, :, 0]
array([ 31., 52., 117., 423., 77., 312., 454., 806., 576.,
581., 403., 1031., 1080., 482., 439., 494., 546., 502.,
453., 362., 385., 367., 344., 169., 25.])
These 25 values correspond to the values in the center of each slice in the first time point. We can also slice on multiple dimensions of the array. For example, if we would like to get the values of all the voxels in the central slice in the very first time-point, we can do:
central_slice_t0 = bold[:, :, 12, 0]
This is a two-dimensional array, with the dimensions of the slice:
central_slice_t0.shape
(64, 64)
Which we can verify by printing out the values inside the array:
print(central_slice_t0)
[[ 0. 0. 0. ... 0. 0. 0.]
[13. 4. 3. ... 16. 3. 6.]
[ 6. 13. 6. ... 13. 26. 7.]
...
[13. 11. 17. ... 16. 6. 5.]
[10. 3. 7. ... 8. 6. 8.]
[ 7. 7. 7. ... 20. 16. 4.]]
bold.shape
(64, 64, 25, 180)
8.2.8. Indexing with conditionals¶
One more way of indexing is to to use logical operations, or conditionals. This allows us to choose values from an array, only if they fulfill certain conditions. For example, if we’d like to exclude measurements with a value of 0 or less, we might perform a logical operation like the following:
larger_than_0 = bold>0
This creates a new array that has the same shape as the original array, but
contains Boolean (True/False) values. Wherever we had a number larger than 0
in the original array, this new array will have the value True and wherever
the numbers in the original array were 0 or smaller, this new array will have
the value False. This is already helpful in some regards, but the next thing
that we can do with this is that we can use this array to index into the
original array. What this does is that it pulls out of the original array only
the values for which larger_than_0 is True and reorganizes these values as a
long one-dimensional array:
bold[larger_than_0]
array([ 6., 11., 5., ..., 12., 4., 14.])
This can be useful, for example, if you would like to calculate statistics of
the original array, but only above some threshold value. For example, if you
would like to calculate the average of the array (using the mean method of the
array) with and without values that are 0 or less:
print(bold.mean())
print(bold[larger_than_0].mean())
145.360578125
148.077239538181
8.2.8.1. Exercise¶
Arrays have a variety of methods attached to them to do calculations. Use the
array method std to calculate the standard deviation of the bold array, and
the standard deviation of just values of the array that are between 1 and 100.
8.2.9. Arithmetic with arrays¶
In addition to storing data from a measurement, and providing access to the this data through indexing, arrays also support a variety of mathematical operations with arrays. For example, you can perform arithmetic operations between an array and a number. Consider for example what happens when we add a single number to an entire array:
bold[32, 32, 12] + 1000
array([2080., 2052., 2056., 2087., 2146., 2147., 2105., 2064., 2128.,
2089., 2095., 2049., 2109., 2051., 2074., 2073., 2112., 2086.,
2090., 2062., 2086., 2023., 2047., 2139., 2065., 2117., 2070.,
2070., 2089., 2074., 2051., 2034., 2096., 2060., 2096., 2076.,
2032., 2067., 2030., 2072., 2056., 2069., 2061., 2054., 2072.,
2072., 2035., 2018., 2116., 2056., 2051., 2084., 2075., 2080.,
2036., 2022., 2076., 2060., 2031., 2079., 2048., 2002., 2055.,
2027., 2014., 2006., 2072., 2003., 2026., 2039., 2096., 2078.,
2025., 2029., 2009., 2065., 2023., 2098., 2045., 2094., 2016.,
2015., 2027., 2020., 2030., 2049., 2034., 2053., 2018., 2038.,
2072., 2020., 2007., 2037., 2082., 2050., 2011., 2027., 1972.,
1992., 1984., 2021., 2018., 2029., 2063., 2070., 2033., 2048.,
2052., 2040., 2007., 1996., 2026., 2011., 2023., 1958., 1982.,
2008., 2059., 2006., 2012., 2042., 2000., 2066., 2026., 2032.,
2009., 2022., 1989., 2020., 2078., 2034., 2036., 1976., 2026.,
1960., 2021., 2009., 2049., 2029., 2065., 2002., 2007., 2031.,
2015., 2044., 2012., 1999., 2002., 1979., 1965., 2011., 2027.,
2013., 2012., 2022., 1981., 2030., 2061., 2056., 2014., 1957.,
1968., 2015., 2100., 1994., 2000., 1973., 1997., 1980., 2026.,
2004., 2008., 1988., 1993., 2042., 2016., 2044., 2002., 2006.])
The result of this operation is that the number is added to every item in the array. Similarly:
bold[32, 32, 12] / 2
array([540. , 526. , 528. , 543.5, 573. , 573.5, 552.5, 532. , 564. ,
544.5, 547.5, 524.5, 554.5, 525.5, 537. , 536.5, 556. , 543. ,
545. , 531. , 543. , 511.5, 523.5, 569.5, 532.5, 558.5, 535. ,
535. , 544.5, 537. , 525.5, 517. , 548. , 530. , 548. , 538. ,
516. , 533.5, 515. , 536. , 528. , 534.5, 530.5, 527. , 536. ,
536. , 517.5, 509. , 558. , 528. , 525.5, 542. , 537.5, 540. ,
518. , 511. , 538. , 530. , 515.5, 539.5, 524. , 501. , 527.5,
513.5, 507. , 503. , 536. , 501.5, 513. , 519.5, 548. , 539. ,
512.5, 514.5, 504.5, 532.5, 511.5, 549. , 522.5, 547. , 508. ,
507.5, 513.5, 510. , 515. , 524.5, 517. , 526.5, 509. , 519. ,
536. , 510. , 503.5, 518.5, 541. , 525. , 505.5, 513.5, 486. ,
496. , 492. , 510.5, 509. , 514.5, 531.5, 535. , 516.5, 524. ,
526. , 520. , 503.5, 498. , 513. , 505.5, 511.5, 479. , 491. ,
504. , 529.5, 503. , 506. , 521. , 500. , 533. , 513. , 516. ,
504.5, 511. , 494.5, 510. , 539. , 517. , 518. , 488. , 513. ,
480. , 510.5, 504.5, 524.5, 514.5, 532.5, 501. , 503.5, 515.5,
507.5, 522. , 506. , 499.5, 501. , 489.5, 482.5, 505.5, 513.5,
506.5, 506. , 511. , 490.5, 515. , 530.5, 528. , 507. , 478.5,
484. , 507.5, 550. , 497. , 500. , 486.5, 498.5, 490. , 513. ,
502. , 504. , 494. , 496.5, 521. , 508. , 522. , 501. , 503. ])
In this case, the number is used to separately divide each one of the elements of the array.
We can also do arithmetic between arrays. For example, we can add the values in this voxel to the items in the central voxel in the neighboring slice:
bold[32, 32, 12] + bold[32, 32, 11]
array([2111., 2079., 2026., 2048., 2009., 1999., 1991., 1926., 2019.,
1940., 1964., 1969., 2015., 1979., 1942., 1976., 1993., 2016.,
1999., 1996., 2054., 1962., 1973., 2017., 1940., 2041., 1966.,
1960., 1957., 2000., 1966., 1961., 1974., 1965., 1953., 2033.,
1973., 2019., 1970., 1946., 1976., 1994., 1974., 1992., 1964.,
2017., 1961., 1946., 2015., 1959., 1959., 1999., 1945., 2031.,
1943., 1957., 2024., 1954., 1932., 2002., 1933., 1935., 2007.,
2012., 1917., 1931., 2032., 1953., 1976., 1951., 1983., 1966.,
1981., 1940., 1944., 1978., 1935., 2001., 1963., 1974., 1965.,
1939., 1997., 1930., 1959., 1952., 1950., 1981., 1982., 1938.,
1967., 1962., 1928., 1906., 1963., 1941., 1927., 1959., 1998.,
1971., 1891., 1975., 1938., 1985., 1939., 1940., 1914., 1939.,
1951., 1927., 1909., 1928., 1980., 1893., 1934., 1894., 1953.,
1901., 1989., 1881., 1928., 1959., 1914., 1962., 1908., 1948.,
1929., 1941., 1917., 1911., 1956., 1943., 1958., 1899., 1961.,
1917., 1933., 1922., 1920., 1911., 1944., 1908., 1916., 1969.,
1913., 1922., 1890., 1937., 1925., 1913., 1876., 1870., 1892.,
1957., 1932., 1930., 1906., 1882., 1913., 1946., 1939., 1947.,
1822., 1861., 1953., 1909., 1911., 1898., 1969., 1832., 1945.,
1878., 1952., 1885., 1918., 1931., 1892., 1913., 1950., 1911.])
When we perform arithmetic operations between an array and a number (or array-scalar operations), the number is separately added to each element. Here, when we perform arithmetic operations between arrays (array-array operations), the operation is instead performed element-by-element. In both cases the result is an array that has the same number of items as the original array (or arrays).
tsnr = bold.mean(-1) / bold.std(-1)
print(tsnr[tsnr.shape[0]//2, tsnr.shape[1]//2, tsnr.shape[2]//2])
27.384290220586703
8.2.9.1. Exercises¶
Creating an array: create an array that contains the sequence of numbers from 1 to 99 in steps of 2: [1, 3, 5, …, 99]
Creating an array of 1’s: create an array of shape (3, 5) containing only the number 1
Find all the items in an array containing numbers that have values that are larger than 0 and smaller or equal to 100
Find all the items in an array that can be divided by 3 with no remainder (hint: the function
np.modexecutes the modulo operation on every item in the array).Generate an array with 100 randomly distributed numbers between 0 and 10 (hint: look at the
np.randomsub-module).
8.2.10. The Scipy library¶
The Numpy array serves as the basis for numerical computing in Python. But it
does only so much. Scientific computing involves a variety of different
algorithms that do more interesting things with numbers. For example, we’d like
to use fancy image processing and signal processing algorithms with our data. Or
rely on various facts about statistical distributions. Over the last 100 years,
scientists and engineers have developed many different algorithms for scientific
computing. In the Python scientific computing ecosystem, many of the fundamental
algorithms are collected together in one library, called Scipy. It provides
everything but the kitchen sink, in terms of basic algorithms for science.
Because it’s such a large collection of things, it is composed of several
different sub-libraries that perform various scientific computing tasks, such as
statistics, image processing, clustering, linear algebra, optimization, etc. We
will revisit some of these in later chapters. For now, as an example, we will
focus on the signal processing sub-library scipy.signal. We import the
sub-library and name it sps:
import scipy.signal as sps
Remember that the BOLD dataset that we were looking at before had 180
time-points. That means that the shape of this data was (64, 64, 25, 180). One
basic signal processing operation is to efficiently and accurately resample a
time-series into a different sampling rate. For example, let’s imagine that we’d
like to resample the data to a slower sampling rate. The original data was
collected with a sampling interval or repetition time (TR) of 2.0 seconds. If we
would like to resample this to half the sampling rate (TR=4.0 seconds), we would
halve the number of samples on the last dimension using the sps.resample
function:
resampled_bold = sps.resample(bold, 90, axis=3)
print(resampled_bold.shape)
(64, 64, 25, 90)
If, instead, we’d like to resample this to twice the sampling rate (TR=1.0), we would double the number of samples.
resampled_bold = sps.resample(bold, 360, axis=3)
print(resampled_bold.shape)
(64, 64, 25, 360)
Although an entire book could be written about Scipy, we will not go into much more detail here. One reason is that Scipy is under the hood of many of the applications that you will see later in the book. For example, the “high-level” libraries that we will use for image-processing (Section 14) and for machine-learning (sklearn) rely on implementations of fundamental computational methods in Scipy. But, unless you are building such tools from scractch, you may not need to use it directly. Nevertheless, it is a wonderful resource to know about, when you do want to build something new that is not already implemented in the existing libraries.
8.2.10.1. Exercise¶
Use the scipy.interpolate sub-library to interpolate the signal in one voxel (take the central voxel, bold[32, 32, 12]) to even higher resolution (TR=0.5 seconds, or 720 samples) using a cubic spline. Hint: Look at the documentation of the scipy.interpolate.interp1d function to choose the method of interpolation and for example usage.
8.2.11. Additional resources¶
For a description of the scientific Python ecosystem, see Fernando Perez, Brian Granger and John Hunter’s paper from 2011 [Perez et al., 2010]. This paper describes in some detail how Python has grown from a general-purpose programming language into a flexible and powerful tool that covers many of the uses that scientists have, through a distributed, eco-system of development. More recent papers describe the tools at the core of the ecosystem: The Numpy library is described in one recent paper [Harris et al., 2020] and the Scipy library is described in another [Virtanen et al., 2020].